Będzie droga rowerowa z Giszowca do Muchowca. Trwają konsultacje

Powstanie droga rowerowa z Giszowca na Muchowiec. Długo wyczekiwana przez mieszkańców inwestycja w końcu będzie realizowana. Jednak na razie trwają tylko przygotowania do projektowania tego ważnego odcinka. Katowiczanie mogą zgłaszać swoje uwagi.

O drodze rowerowej z Giszowca w kierunku Doliny Trzech Stawów zrobiło się głośno pryz okazji drogowej inwestycji. Okazało się, że podczas już realizowanej przebudowy węzła dróg krajowych 86 i 81 (ulic Pszczyńskiej i 73 Pułku Piechoty), na którą miasto wyda niecałe 250 mln zł, nie powstanie droga rowerowa. Teraz urzędnicy podjęli pierwsze kroki, żeby zbudować połączenie rowerowe w stronę centrum miasta, a przede wszystkim terenów rekreacyjnych.

PRZECZYTAJ TEŻ: Rusza przebudowa skrzyżowania DK 86 i DK 81. To inwestycja za prawie 250 mln zł

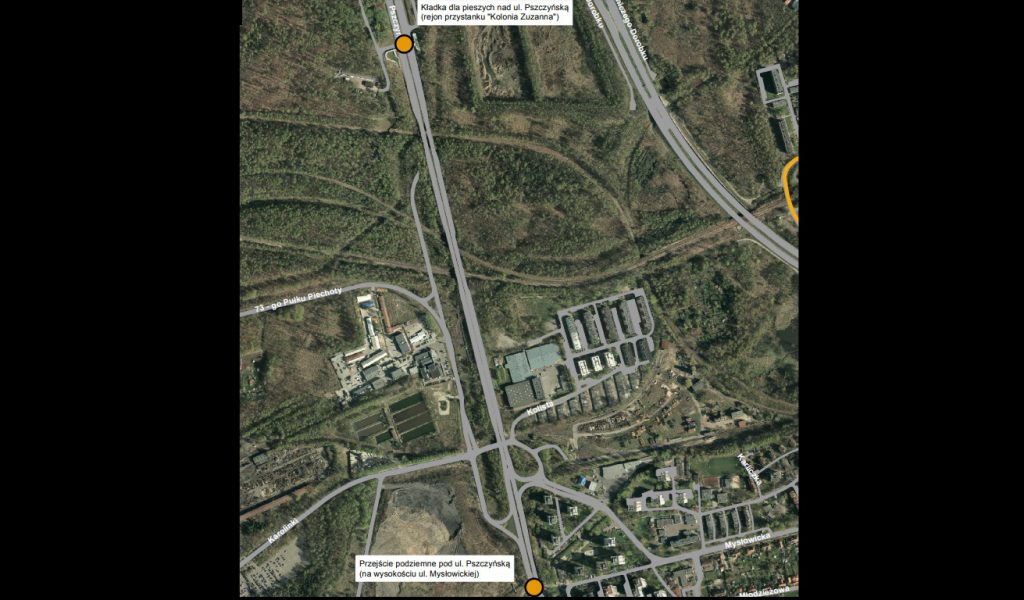
Na razie przejazd w tamtym kierunku nie należy do łatwych. Jadąc wzdłuż ul. Pszczyńskiej trzeba przedostać się przez tory. Do wyboru jest już zniszczony wiadukt tuż przy bardzo ruchliwej trasie DK 86 lub przejście dołem przez kilka torów. Dzięki nowej drodze dojazd ma być znacznie bardziej komfortowy. Na razie trwają konsultacje społeczne, które są szansą dla mieszkańców do zgłaszania uwag. Do zaprojektowania jest spory odcinek. Droga ma rozpoczynać się przy przejściu podziemnym na wysokości ul. Mysłowickiej (po zachodniej stronie ul. Pszczyńskiej) i kończyć na istniejącej kładce na wysokości przystanku autobusowego Kolonia Zuzanna. Konsultacje potrwają jeszcze przez niecały tydzień, do 22 sierpnia. Swoją opinię wyrazić można TUTAJ. Jak poinformowało nas biuro prasowe,  zamówienie koncepcji przebiegu nastąpi w IV kwartale br. Rowerzyści mają pojechać nową drogą w 2019 r. Koszt samej koncepcji ma wynieść ok. 200 tys. zł brutto.